Advertisements
Advertisements
प्रश्न
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
उत्तर
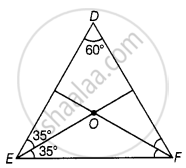
(i) As we know,
∠D + ∠E + ∠F = 180° ......[Angle sum property of a triangle]
⇒ 60° + 70° + ∠F = 180° ......[∵ ∠D = 60° and ∠E = 70°]
⇒ ∠F = 180° – 130°
⇒ ∠F = 50°
(ii) Now, as FO is the bisector of ∠F
So, ∠EFO = `(∠F)/2 = 50^circ/2` = 25°
And ∠OEF = `(∠E)/2 = 70^circ/2` = 35° ......[∵ ∠D = 60° and ∠E = 70°]
In ΔEOF, ∠EOF + ∠OEF + ∠OFE = 180° ......[Angle sum property of a triangle]
⇒ ∠EOF + 35° + 25° = 180°
⇒ ∠EOF = 180° – 60°
⇒ ∠EOF = 120°
APPEARS IN
संबंधित प्रश्न
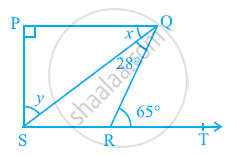
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
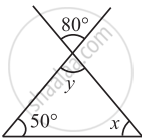
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x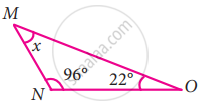
In the following triangle, find the value of x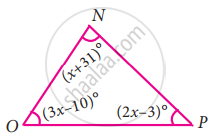
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
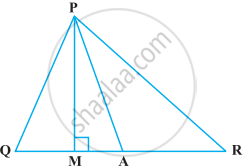
In the given figure, PB = PD. The value of x is ______.
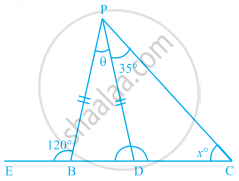
It is possible to have a triangle in which two of the angles are right angles.
It is possible to have a triangle in which each angle is greater than 60°.
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
