Advertisements
Advertisements
Question
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
Solution
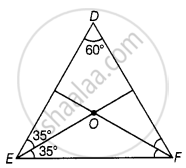
(i) As we know,
∠D + ∠E + ∠F = 180° ......[Angle sum property of a triangle]
⇒ 60° + 70° + ∠F = 180° ......[∵ ∠D = 60° and ∠E = 70°]
⇒ ∠F = 180° – 130°
⇒ ∠F = 50°
(ii) Now, as FO is the bisector of ∠F
So, ∠EFO = `(∠F)/2 = 50^circ/2` = 25°
And ∠OEF = `(∠E)/2 = 70^circ/2` = 35° ......[∵ ∠D = 60° and ∠E = 70°]
In ΔEOF, ∠EOF + ∠OEF + ∠OFE = 180° ......[Angle sum property of a triangle]
⇒ ∠EOF + 35° + 25° = 180°
⇒ ∠EOF = 180° – 60°
⇒ ∠EOF = 120°
APPEARS IN
RELATED QUESTIONS
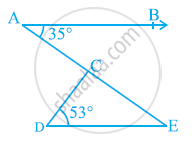
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
Find the value of the unknown x in the following diagram:
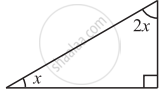
In the following triangle, find the value of x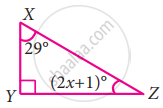
In the following triangle, find the value of x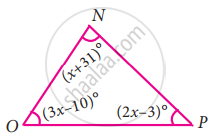
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
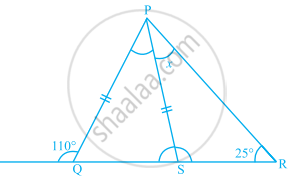
In the given figure, PQ = PS. The value of x is ______.
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
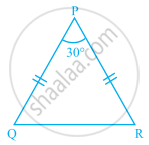
In the given figure, if ST = SU, then find the values of x and y.

