Advertisements
Advertisements
प्रश्न
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
उत्तर
Given, 3∠P = 4∠Q = 6∠R
Then, ∠P = `6/3`∠R = 2∠R
∠Q = `6/4`∠R = `3/2`∠R
In ΔPQR, ∠P + ∠Q + ∠R = 180° .....[Angle sum property of a triangle]
⇒ 2∠R + `3/2`∠R + ∠R = 180°
⇒ 3∠R + `3/2`∠R = 180°
⇒ 6∠R + 3∠R = 180° × 2 ......[On taking LCM in LHS]
⇒ 9∠R = 360°
⇒ ∠R = `360^circ/9` = 40°
∴ ∠P = 2∠R = 2 × 40° = 80°
And ∠Q = `3/2`∠R = `3/2` × 40° = 60°
Hence, all the angles of the triangle are 80°, 60° and 40°.
APPEARS IN
संबंधित प्रश्न
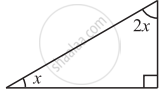
Find the value of the unknown x in the following diagram:
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
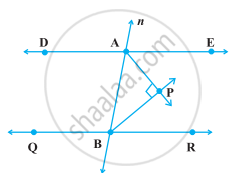
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
Prove that a triangle must have atleast two acute angles.
In a right-angled triangle, the angles other than the right angle are ______.
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
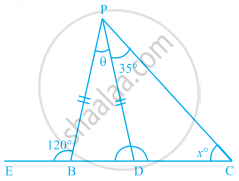
In the given figure, PB = PD. The value of x is ______.
It is possible to have a triangle in which each angle is less than 60°.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
