Advertisements
Advertisements
प्रश्न
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
उत्तर
In ∆RST, Let ∠R = x.
Then given ∠S is 10° greater than ∠R
∴ ∠S = x + 10°
Also given ∠T is 5° less than ∠S.
So ∠T = ∠S – 5°
= (x + 10)° – 5°
= x + 10° – 5°
By angle sum property of triangle, sum of three angles = 180°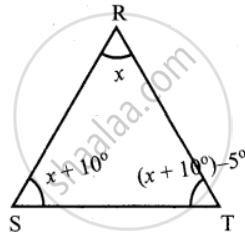
∠R + ∠S + ∠T = 180°
x + x + 10° + x + 5° = 180°
3x + 15° = 180°
3x = 180° – 15°
x = `(165^circ)/3` = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°
APPEARS IN
संबंधित प्रश्न
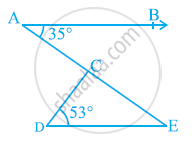
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
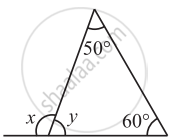
Find the value of the unknowns x and y in the following diagram:
In the following triangle, find the value of x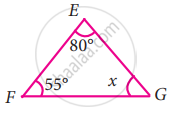
In the given figure, which of the following statement is true?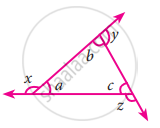
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
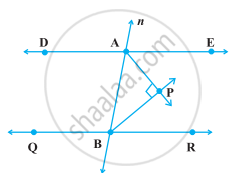
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
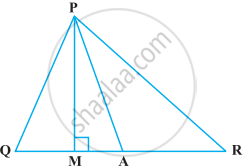
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
