Advertisements
Advertisements
प्रश्न
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
उत्तर
It is given that the triangle has its angles as 53°, 64° and 63°.
Upon adding these, we get
⇒ Sum of the three angles = 53° + 64° + 63°
⇒ Sum of the three angles = 180° ...(i)
We know, that the sum of all the angles of a triangle is equal to 180°.
Also, from (i), we find out that the sum of the given angles of the triangle is equal to 180°.
Thus, infinite number of triangles can be drawn having angles as 53°, 64° and 63°.
APPEARS IN
संबंधित प्रश्न
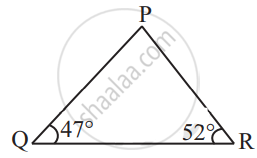
In the given figure find m∠P.
In the following triangle, find the value of x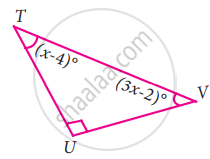
Prove that a triangle must have atleast two acute angles.
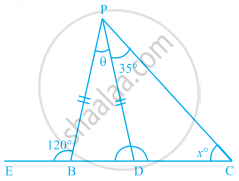
In the given figure, PB = PD. The value of x is ______.
If two angles of a triangle are 60° each, then the triangle is ______.
The sum of the measures of three angles of a triangle is greater than 180°.
It is possible to have a triangle in which each angle is greater than 60°.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
