Advertisements
Advertisements
प्रश्न
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
उत्तर
Given Consider a line l and a point P.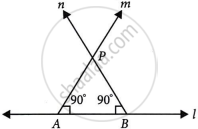
Construction: Draw two intersecting lines passing through the point P and which is perpendicular to l.
To prove: Only one perpendicular line can be drawn through a given point i.e., to prove ∠P = 0°.
Proof: In ΔAPB, ∠A + ∠P + ∠B = 180° ...[By angle sum property of a triangle is 180°]
⇒ 90 + ∠P + 90° = 180°
⇒ ∠P = 180° – 180°
∴ ∠P = 0°
So, lines n and m coincide.
Hence, only one perpendicular line can be drawn through a given point.
APPEARS IN
संबंधित प्रश्न
Find the value of the unknown x and y in the following diagram:

In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
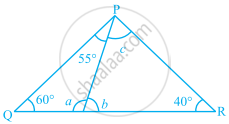
In the given figure, find the values of a, b and c
I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
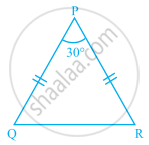
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
