Advertisements
Advertisements
Question
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
Solution
Given Consider a line l and a point P.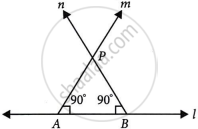
Construction: Draw two intersecting lines passing through the point P and which is perpendicular to l.
To prove: Only one perpendicular line can be drawn through a given point i.e., to prove ∠P = 0°.
Proof: In ΔAPB, ∠A + ∠P + ∠B = 180° ...[By angle sum property of a triangle is 180°]
⇒ 90 + ∠P + 90° = 180°
⇒ ∠P = 180° – 180°
∴ ∠P = 0°
So, lines n and m coincide.
Hence, only one perpendicular line can be drawn through a given point.
APPEARS IN
RELATED QUESTIONS
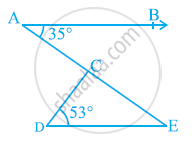
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
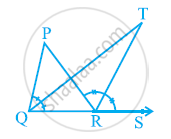
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
The sum of the measures of three angles of a triangle is greater than 180°.
If two triangles are congruent, then the corresponding angles are equal.
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

