Advertisements
Advertisements
Question
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
Solution
Let the third angle be x. Then, the other two angles are 4x and 4x, respectively.
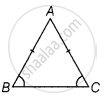
We know that, the sum of all three angles in a triangle is 180°.
i.e., ∠A + ∠B + ∠C = 180°
⇒ x + 4x + 4x = 180°
⇒ 9x = 180°
⇒ x = `180^circ/9` = 20°
Hence, the three angles are 4x = 4 × 20° = 80°, 4x = 4 × 20° = 80° and x = 20°.
APPEARS IN
RELATED QUESTIONS
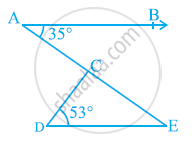
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
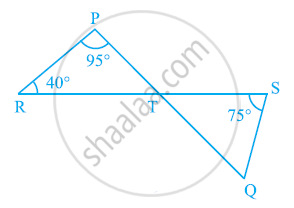
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
Find the value of the unknown x and y in the following diagram:
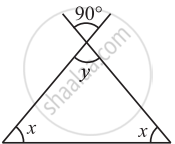
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
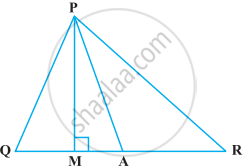
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
If two triangles are congruent, then the corresponding angles are equal.
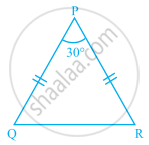
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.