Advertisements
Advertisements
प्रश्न
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
उत्तर
Let the third angle be x. Then, the other two angles are 4x and 4x, respectively.
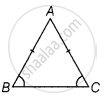
We know that, the sum of all three angles in a triangle is 180°.
i.e., ∠A + ∠B + ∠C = 180°
⇒ x + 4x + 4x = 180°
⇒ 9x = 180°
⇒ x = `180^circ/9` = 20°
Hence, the three angles are 4x = 4 × 20° = 80°, 4x = 4 × 20° = 80° and x = 20°.
APPEARS IN
संबंधित प्रश्न
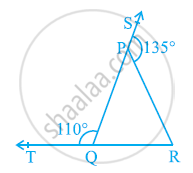
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
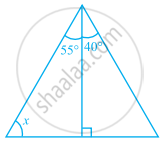
In the given figure, find the value of x.
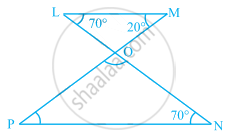
In the given figure, find the measures of ∠PON and ∠NPO.
Find the values of x and y in the given figure.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
