Advertisements
Advertisements
प्रश्न
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
उत्तर
Let the third angle be x. Then, the other two angles are 4x and 4x, respectively.
We know that, the sum of all three angles in a triangle is 180°.
i.e., ∠A + ∠B + ∠C = 180°
⇒ x + 4x + 4x = 180°
⇒ 9x = 180°
⇒ x = `180^circ/9` = 20°
Hence, the three angles are 4x = 4 × 20° = 80°, 4x = 4 × 20° = 80° and x = 20°.
APPEARS IN
संबंधित प्रश्न
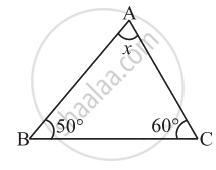
Find the value of the unknown x in the following diagram:
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
In the given figure, which of the following statement is true?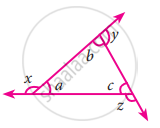
Can a triangle have two obtuse angles? Give reason for your answer.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
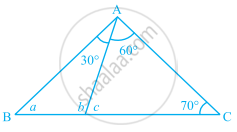
In the given figure, find the values of a, b and c.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
In the given figure, if ST = SU, then find the values of x and y.

