Advertisements
Advertisements
प्रश्न
Can a triangle have two obtuse angles? Give reason for your answer.
उत्तर
We know, the sum of three angles of a triangle is equal to 180°.
Also, an obtuse angle is one whose value is greater than 90° but less than 180°.
If the triangle has two obtuse angles, then there are at least two angles which are 91° each.
On adding these two angles,
Sum of the two angles = 91° + 91°
⇒ Sum of the two angles = 182°
This already exceeds the sum of three angles of the triangle, even without considering the third angle.
Again, if we consider the case where one angle of the triangle is 90°, we have a right-angled triangle. The rest two angles must be less than 90° each so as to satisfy the property of a triangle, which states that the sum of the three angles of a triangle should be equal to 180°.
Thus, a triangle cannot have two obtuse angles.
APPEARS IN
संबंधित प्रश्न
Find the value of the unknown x in the given diagram:
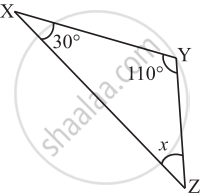
Find the value of the unknown x in the following diagram:
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B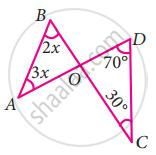
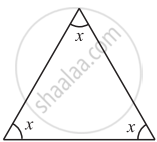
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
Can a triangle have all angles less than 60°? Give reason for your answer.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
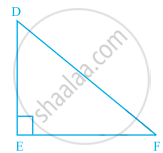
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
