Advertisements
Advertisements
प्रश्न
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B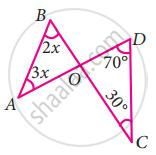
उत्तर
In ∆AOB and ∆DOC,
∠AOB = ∠DOC ...[∵ Vertically opposite angles are equal]
Let ∠AOB = ∠DOC = y
By angle sum property of a triangle we have
∠A + ∠B + ∠AOB = ∠D + ∠C + ∠DOC = 180°
3x + 2x + y = 70° + 30° + y = 180°
5x + y = 100° + y = 180°
Here 5x + y = 100° + y
5x = 100° + y – y
5x = 100°
x = `(100^circ)/5` = 20°
∠A = 3x = 3 × 20 = 60°
∠B = 2x = 2 × 20 = 40°
∠A = 60°
∠B = 40°
APPEARS IN
संबंधित प्रश्न
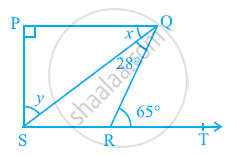
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
Find the value of the unknown x and y in the following diagram:
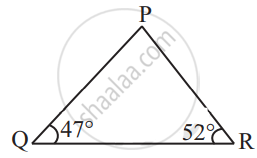
In the given figure find m∠P.
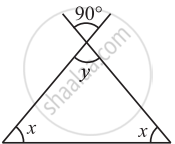
In the following triangle, find the value of x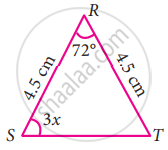
In the given figure, which of the following statement is true?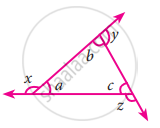
Can a triangle have two obtuse angles? Give reason for your answer.
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
In the given figure, find the values of a, b and c.
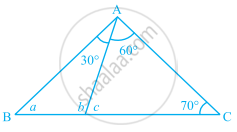
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

