Advertisements
Advertisements
प्रश्न
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
उत्तर
Given In ∆ABC, produce SC to D and the bisectors of ∠ABC and ∠ACD meet at point T.
To prove `∠BTC = 1/2 ∠BAC`
Proof: In ∆ABC, ∠C is an exterior angle.
∴ ∠ACD = ∠ABC + ∠CAB ...[Exterior angle of a triangle is equal to the sum of two opposite angles]
⇒ `1/2 ∠ACD = 1/2 ∠CAB + 1/2 ∠ABC` ...[Dividing both sides by 2]
⇒ `∠TCD = 1/2 ∠CAB + 1/2 ∠ABC` ...(i) `[∵ "CT is a bisector of "∠ACD ⇒ 1/2 ∠ACD = ∠TCD]`
In ∆BTC, ∠TCD = ∠BTC + ∠CBT ...[Exterior angle of a triangle is equal to the sum of two opposite interior angles]
⇒ `∠TCD = ∠BTC + 1/2 ∠ABC` ...(ii) `[∵ "BT bisects of" ∠ABC ⇒ ∠CBT = 1/2 ∠ABC]`
From equations (i) and (ii),
`1/2 ∠CAB + 1/2 ∠ABC = ∠BTC + 1/2 ∠ABC`
⇒ `∠BTC = 1/2 ∠CAB`
or `∠BTC = 1/2 ∠BAC`
APPEARS IN
संबंधित प्रश्न
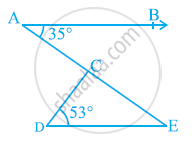
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
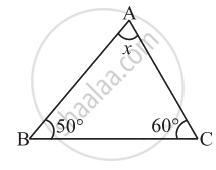
Find the value of the unknown x in the following diagram:
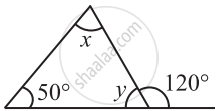
Find the value of the unknown x and y in the following diagram:
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S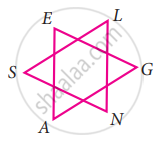
In the given figure, which of the following statement is true?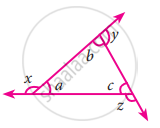
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
It is possible to have a triangle in which each angle is less than 60°.
It is possible to have a triangle in which each angle is greater than 60°.
