Advertisements
Advertisements
Question
In the following triangle, find the value of x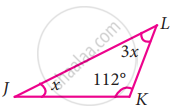
Solution
Let ∠J = x and ∠L = 3x
By angle sum property of triangle we have
∠J + ∠K + ∠L = 180°
x + 112° + 3x = 180°
4x = 180° – 112°
x = 68°
x = `(68^circ)/4`
x = 17°
APPEARS IN
RELATED QUESTIONS
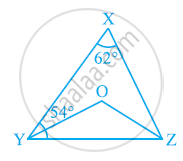
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
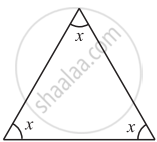
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x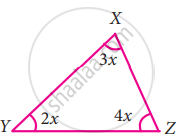
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Can a triangle have all angles less than 60°? Give reason for your answer.
Can a triangle have two obtuse angles? Give reason for your answer.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
