Advertisements
Advertisements
Question
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
Options
80°
20°
40°
30°
Solution
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to 40°.
Explanation:
Given, ∠BAD = ∠DAC = 50° ......[∵ AD bisects ∠A and ∠A = 100°]
And ∠BDA = ∠ADC = 90° ......[∵ AD ⊥ BC]
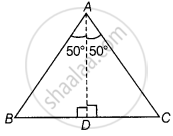
Now, In ∆ABC,
∠ABD + ∠BAD + ∠BDA = 180° ......[Angle sum property of a triangle]
⇒ ∠ABD + 50° + 90° = 180°
⇒ ∠ABD + 140° = 180°
⇒ ∠ABD = 180° – 140°
⇒ ∠ABD = 40°
APPEARS IN
RELATED QUESTIONS
In the following triangle, find the value of x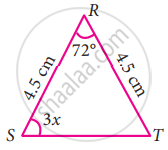
In the following triangle, find the value of x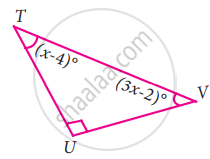
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
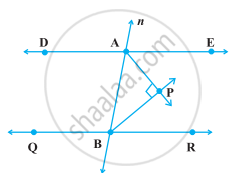
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
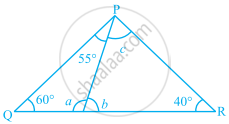
In the given figure, find the values of a, b and c
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
