Advertisements
Advertisements
Question
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
Solution
Given In ΔABC, ∠A = 90° and AL ⊥ BC
To prove ∠BAL = ∠ACB
Proof In ΔABC and ΔLAC, ∠BAC = ∠ALC [Each 90°] ...(i)
And ∠ABC = ∠ABL [Common angle] ...(ii)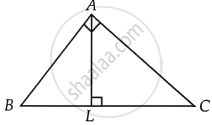
On adding equation (i) and (ii), we get
∠BAC + ∠ABC = ∠ALC + ∠ABL ...(iii)
Again, in ΔABC,
∠BAC + ∠ACB + ∠ABC = 180° ...[Sum of all angles of a triangle is 180°]
⇒ ∠BAC + ∠ABC = 180° – ∠ACB ...(iv)
In ΔABL,
∠ABL + ∠ALB + ∠BAL = 180° ...[Sum of all angles of a triangle is 180°]
⇒ ∠ABL + ∠ALC = 180° – ∠BAL ...[∴ ∠ALC = ∠ALB = 90°] ...(v)
On substituting the value from equations (iv) and (v) in equation (iii), we get
180° – ∠ACS = 180° – ∠SAL
⇒ ∠ACB = ∠BAL
Hence proved.
APPEARS IN
RELATED QUESTIONS
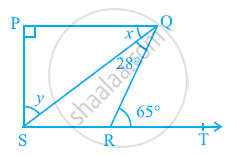
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
In the given figure, which of the following statement is true?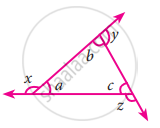
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
In the given figure, find the measures of ∠PON and ∠NPO.
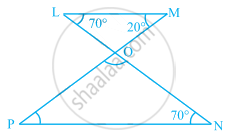
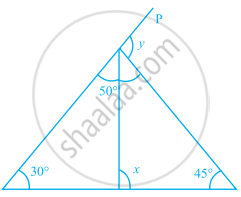
Find the values of x and y in the given figure.