Advertisements
Advertisements
प्रश्न
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
उत्तर
Given In ΔABC, ∠A = 90° and AL ⊥ BC
To prove ∠BAL = ∠ACB
Proof In ΔABC and ΔLAC, ∠BAC = ∠ALC [Each 90°] ...(i)
And ∠ABC = ∠ABL [Common angle] ...(ii)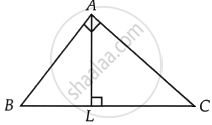
On adding equation (i) and (ii), we get
∠BAC + ∠ABC = ∠ALC + ∠ABL ...(iii)
Again, in ΔABC,
∠BAC + ∠ACB + ∠ABC = 180° ...[Sum of all angles of a triangle is 180°]
⇒ ∠BAC + ∠ABC = 180° – ∠ACB ...(iv)
In ΔABL,
∠ABL + ∠ALB + ∠BAL = 180° ...[Sum of all angles of a triangle is 180°]
⇒ ∠ABL + ∠ALC = 180° – ∠BAL ...[∴ ∠ALC = ∠ALB = 90°] ...(v)
On substituting the value from equations (iv) and (v) in equation (iii), we get
180° – ∠ACS = 180° – ∠SAL
⇒ ∠ACB = ∠BAL
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the value of the unknown x in the following diagram:
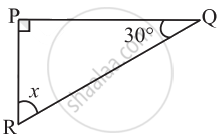
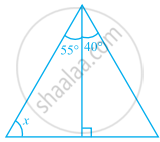
In the following triangle, find the value of x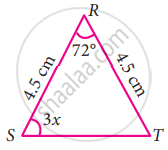
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B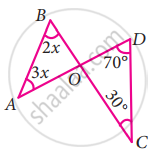
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
In the given figure, find the value of x.
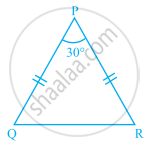
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
