Advertisements
Advertisements
प्रश्न
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
उत्तर
Given, ratio of angles is 2 : 3 : 4
Let the angles of the triangle be 2x, 3x and 4x.
So, 2x + 3x + 4x = 180° ...[Sum of angles of triangle is 180°]
9x = 180°
x = `(180^circ)/9`
x = 20°
Therefore, 2x = 2 × 20° = 40°
3x = 3 × 20° = 60°
And 4x = 4 × 20° = 80°
Hence, the angle of the triangle are 40°, 60° and 80°.
APPEARS IN
संबंधित प्रश्न
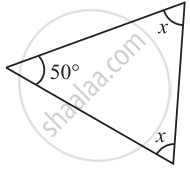
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x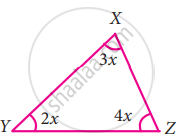
In the following triangle, find the value of x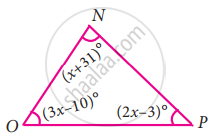
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B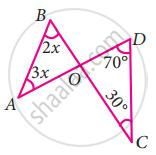
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S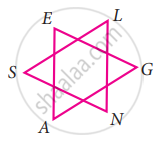
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Can a triangle have two obtuse angles? Give reason for your answer.
If two angles of a triangle are 60° each, then the triangle is ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
If two triangles are congruent, then the corresponding angles are equal.
