Advertisements
Advertisements
प्रश्न
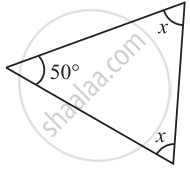
Find the value of the unknown x in the following diagram:
उत्तर
The sum of all interior angles of a triangle is 180°. By using this property, these problems can be solved as follows:
50° + x + x = 180°
50° + 2x = 180°
2x = 180° − 50°
2x = 130°
x = `(130°)/2`
x = 65°
APPEARS IN
संबंधित प्रश्न
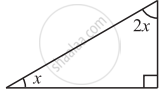
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x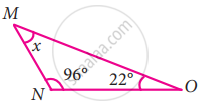
In the given figure, which of the following statement is true?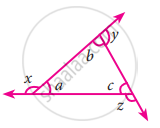
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Can a triangle have all angles less than 60°? Give reason for your answer.
Can a triangle have two obtuse angles? Give reason for your answer.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In a right-angled triangle, the angles other than the right angle are ______.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
It is possible to have a triangle in which each angle is less than 60°.
