Advertisements
Advertisements
प्रश्न
Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
उत्तर
Given Two lines m and n are parallel and another two lines p and q are respectively perpendicular to m and n.
i.e., p ⊥ m, p ⊥ n, q ⊥ m, q ⊥ n
To prove p || g
Proof Since, m || n and p is perpendicular to m and n.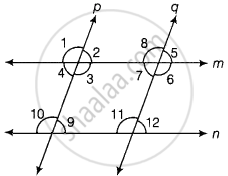
∴ ∠1 = ∠10 = 90° ...[Corresponding angles]
Similarly, ∠2 = ∠9 = 90° ...[Corresponding angles]
∴ ∠4 = ∠9 = 90° and ∠3 = ∠10 = 90° ...[Alternative interior angles] [∵ p ⊥ m and p ⊥ n]
Similarly, if m || n and q is perpendicular to m and n.
Then, ∠7 = 90° and ∠11 = 90°
Now, ∠3 + ∠7 = 90° + 90° = 180°
So, sum of two interior angles is supplementary.
We know that, if a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Hence, p || g.
APPEARS IN
संबंधित प्रश्न
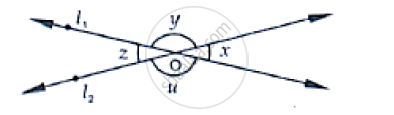
In the below fig, lines �1 and �2 intersect at O, forming angles as shown in the figure. If x = 45, Find the values of x, y, z and u.
If one of the four angles formed by two intersecting lines is a right angle, then show that
each of the four angles is a right angle.
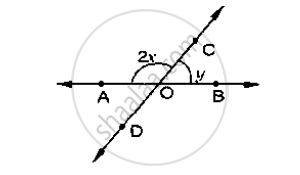
In the below fig, rays AB and CD intersect at O.
Determine y when x = 60°
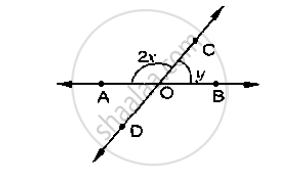
In the below fig, rays AB and CD intersect at O
Determine x when y =40
Two straight line AB and CD intersect one another at the point O. If ∠AOC + ∠COB + ∠BOD = 274°, then ∠AOD =
Consider the following statements:
When two straight lines intersect:
(i) adjacent angles are complementary
(ii) adjacent angles are supplementary
(iii) opposite angles are equal
(iv) opposite angles are supplementary
Of these statements
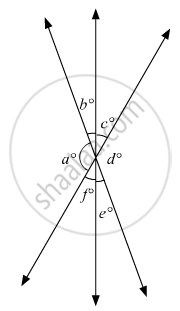
In the given figure, which of the following statements must be true?
(i) a + b = d + c
(ii) a + c + e = 180°
(iii) b + f = c + e
Two lines AB and CD intersect at O. If ∠AOC + ∠COB + ∠BOD = 270°, then ∠AOC =
Look at the picture given below. Decide whether the lines given in picture is parallel or perpendicular to each other and write the answer in the box.

Two parallel lines meet each other at some point.
