Advertisements
Advertisements
प्रश्न
Find the value of the unknown x in the following diagram:
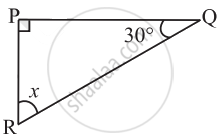
उत्तर
The sum of all interior angles of a triangle is 180°. By using this property, these problems can be solved as follows:
x + 90° + 30° = 180°
x + 120° = 180°
x = 180° − 120°
x = 60°
APPEARS IN
संबंधित प्रश्न
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B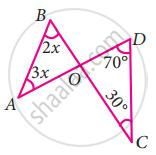
Can a triangle have two obtuse angles? Give reason for your answer.
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
The sum of the measures of three angles of a triangle is greater than 180°.
It is possible to have a triangle in which each angle is less than 60°.
In the given figure, find the measures of ∠x and ∠y.
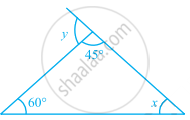
The angles of a triangle are in the ratio 2:3:5. Find the angles.
In the given figure, if ST = SU, then find the values of x and y.

