Advertisements
Advertisements
प्रश्न
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
उत्तर
Given in ∆XYZ, ∠X : ∠Z = 5 : 4
Let ∠X = 5x, and ∠Z = 4x given ∠Y = 72°
By the angle sum property of triangle sum of three angles of a triangle is 180°.
∠X + ∠Y + ∠Z = 180°
5x + 72 + 4x = 180°
5x + 4x = 180° – 72°
9x = 108°
x = `(108^circ)/9` = 12°
∠X = 5x = 5 × 12° = 60°
∠Z = 4x = 4 × 12° = 48°
∴ ∠X = 60°
∠Z = 48°
APPEARS IN
संबंधित प्रश्न
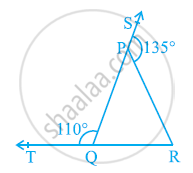
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
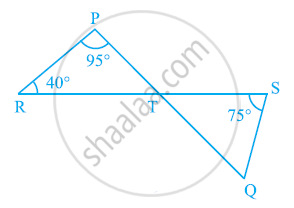
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
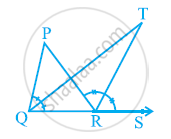
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
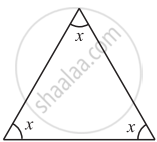
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x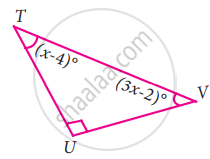
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
In a right-angled triangle, the angles other than the right angle are ______.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
It is possible to have a triangle in which two of the angles are right angles.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
