Advertisements
Advertisements
प्रश्न
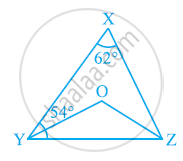
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
उत्तर
As the sum of all interior angles of a triangle is 180º, therefore, for ΔXYZ,
∠X + ∠XYZ + ∠XZY = 180º
62º + 54º + ∠XZY = 180º
∠XZY = 180º − 116º
∠XZY = 64º
∠OZY = 64/2 = 32º (OZ is the angle bisector of ∠XZY)
Similarly, ∠OYZ = 54/2 = 27°
Using angle sum property for ΔOYZ, we obtain
∠OYZ + ∠YOZ + ∠OZY = 180º
27º + ∠YOZ + 32º = 180º
∠YOZ = 180º − 59º
∠YOZ = 121º
APPEARS IN
संबंधित प्रश्न
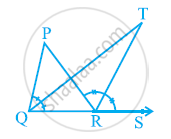
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
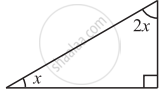
Find the value of the unknown x in the following diagram:
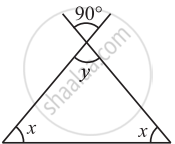
Find the value of the unknown x and y in the following diagram:
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is ______.
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
If two angles of a triangle are 60° each, then the triangle is ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
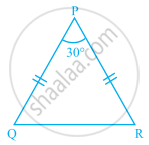
In the given figure, if ST = SU, then find the values of x and y.

