Advertisements
Advertisements
प्रश्न
Identify the centroid of ∆PQR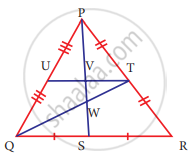
उत्तर
In ∆PQR, PT = TR ⇒ QT is a median from vertex Q.
QS = SR ⇒ PS is a median from vertex P.
QT and PS meet at W and therefore W is the centroid of ∆PQR.
APPEARS IN
संबंधित प्रश्न
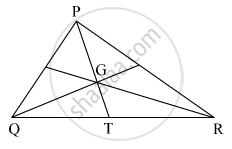
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
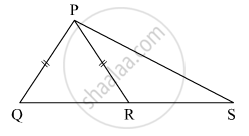
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
The medians of a triangle cross each other at _______
In any triangle the centroid and the incentre are located inside the triangle
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA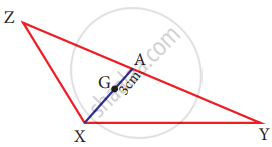
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DO = 8, then FD = ?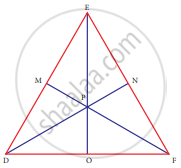
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
