Advertisements
Advertisements
प्रश्न
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
विकल्प
Median
Angle bisector
Altitude
Hypotenuse
उत्तर
Median
Explanation:
Consider ΔABC in which AD divides BC in the ratio 1:1.
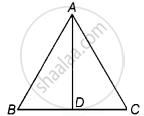
Now, BD:DC = 1:1
⇒ `(BD)/(DC) = 1/1`
∴ BD = DC
Since, AD divides BC into two equal parts.
Hence, AD is the median.
APPEARS IN
संबंधित प्रश्न
The length of hypotenuse of a right angled triangle is 15. Find the length of median of its hypotenuse.
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
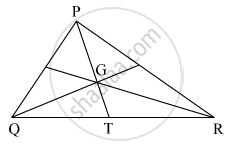
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
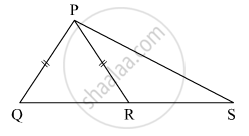
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
The medians of a triangle cross each other at _______
The centroid of a triangle divides each medians in the ratio _______
In any triangle the centroid and the incentre are located inside the triangle
The centroid, orthocentre, and incentre of a triangle are collinear
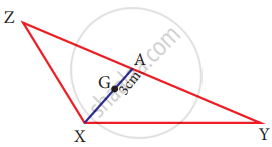
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA