Advertisements
Advertisements
Question
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

Solution
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) In ΔAMC and ΔANB
AB = AC ...[ Given ] ...(1)
BM = CN ....[ Given ] ...(2)
Subtracting (2) from (1), we have
AB - BM = AC - CN
⇒ AM = AN ...(3)
(ii) Consider the triangles AMC and ANB
AC = AB ...[ given ]
∠AMC = ∠ANB ...[ common 90° ]
AM = AN ....[ from ( 3 ) ]
∴ By the Side-Angel-Side Criterion of congruence, we have ΔAMC ≅ ΔANB
APPEARS IN
RELATED QUESTIONS
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
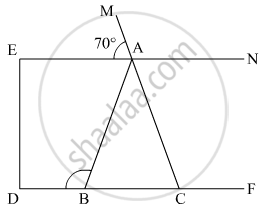
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
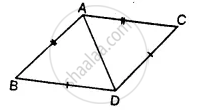
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.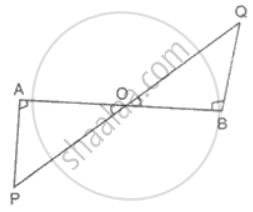
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.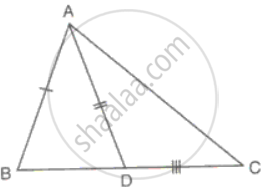
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
