Advertisements
Advertisements
प्रश्न
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

उत्तर
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) In ΔAMC and ΔANB
AB = AC ...[ Given ] ...(1)
BM = CN ....[ Given ] ...(2)
Subtracting (2) from (1), we have
AB - BM = AC - CN
⇒ AM = AN ...(3)
(ii) Consider the triangles AMC and ANB
AC = AB ...[ given ]
∠AMC = ∠ANB ...[ common 90° ]
AM = AN ....[ from ( 3 ) ]
∴ By the Side-Angel-Side Criterion of congruence, we have ΔAMC ≅ ΔANB
APPEARS IN
संबंधित प्रश्न
If ΔPQR≅ ΔEFD, then ∠E =
Which of the following is not a criterion for congruence of triangles?
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
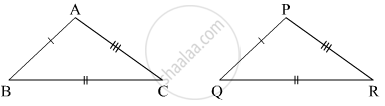
By ______ test
Δ ABC ≅ ΔPQR
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
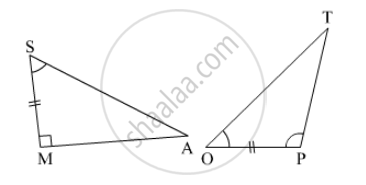
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
Which of the following rule is not sufficient to verify the congruency of two triangles
The congruent figures super impose each other completely.
