Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
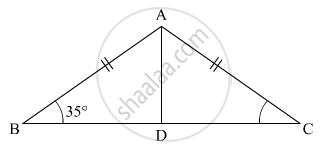
विकल्प
55°
70°
35°
110°
उत्तर
It is given that ∠B = 35°, AB=AC and Ad is the median of BC

We know that in isosceles triangle the median from he vertex to the unequal side divides it into two equal part at right angle.
Therefore,
∠ADB = 90°
∠B = ∠ADB + ∠A= 180° (Property of triangle)
35° + 90° +∠A = 180°
∠A = 180° - 125°
∠A = 55°
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In ΔPQR ≅ ΔEFD then ED =
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
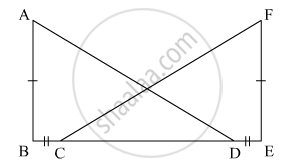
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles

ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
