Advertisements
Advertisements
प्रश्न
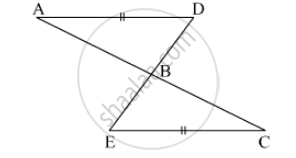
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
उत्तर
Given:
ABCD is a parallelogram, where BE = CE
To prove:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
a. In ΔDCE and ΔLBE
∠DCE = ∠EBL ....[DC || AB, alternate angles]
CE = BE ....[given]
∠DEC = ∠LEB ....[vertically opposite angles]
∴ By Angle-Side-Angle criterion of congruence,
ΔDCE ≅ ΔLBE
The corresponding parts of the congruent triangles are congruent.
∴ DC = LB ....(1)
b. DC = AB ....(2)[opposite sides of a parallelogram]
From (1) and (2),
AB = BL ....(3)
c. Al = AB + BL
⇒ AL = Ab + AB ....[From (3)]
⇒ AL = 2AB
⇒ Al = 2DC. ....[From (2)]
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
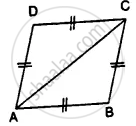
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.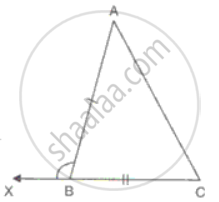
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.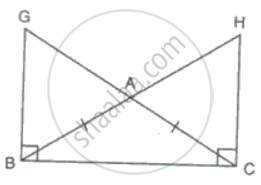
Prove that
(i) BG = CH
(ii) AG = AH
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
