Advertisements
Advertisements
प्रश्न
Prove that the medians of an equilateral triangle are equal.
Advertisements
उत्तर
Given to prove that the medians of an equilateral triangle are equal
Median: The line joining the vertex and midpoint of opposite side.
Now, consider an equilateral triangle ABC
Let D,E,F are midpoints of , BC CAand . AB
Then, , AD BE and CF are medians of . Δ ABC
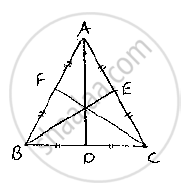
Now ,
D is midpoint of BC⇒ BD = DC =`(BC)/2`
Similarly ,` CE=EA=(AC)/2`
`AF= FB=(AB)/2`
Since Δ ABC is an equilateral traingle ⇒ AB=BC= CA .............(1)
`BD=DC=CE=EA=AF=FB= (BC)/2=(AC)/2 (AB)/2` ..............(2)
And also , ∠ ABC= ∠ BCA=∠CAB=60° ..................(3)
Now, consider Δ ABD and Δ BCE
AB=BC [from (1)]
BD= CE [from (2)]
∠ ABD= ∠ BCE [from (3)] [∠ ABD and ∠ ABC and ∠ BCE and BCA aare same ]
So, from SAS congruence criterion , we have
Δ ABD ≅ Δ BCE
AD= BE ........................(4)
[corresponding parts of congruent triangles are equal]
Now, consider ΔBCE and Δ CAF,
BC = CA [from (1)]
∠BCE =∠ CAF [from (3)]
[∠ BCE and ∠ BCA and ∠ CAF annd ∠ CAB are same ]
CE=AF [from (2)]
So, from SAS congruence criterion, we have Δ BCE≅ Δ CAF
⇒ BE=CF ..........................(5)
[Corresponding parts of congruent triangles are equal ]
From (4) and (5), we have
AD =BE= CF
⇒Median AD = Median BE = Median CF
∴The medians of an equilateral triangle are equal
∴Hence proved
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
Write the sum of the angles of an obtuse triangle.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
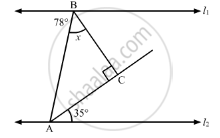
In the given figure, what is z in terms of x and y?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
In the given figure, if l1 || l2, the value of x is
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
