Advertisements
Advertisements
प्रश्न
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then
विकल्प
x = 55°, y = 40°
x = 50°, y = 45°
x = 60°, y = 35°
x = 35°, y = 60°
Advertisements
उत्तर
In the given figure and AB|| CD , ∠APR = 25°, ∠RQC = 30V , and ∠CQF = 65°
We need to find the value of x and y
Here, we draw a line ST parallel to AB, i.e AB || ST
Also, using the property, “two lines parallel to the same line are parallel to each other”
As,
AB || ST
AB || CD
Thus, CD || ST
Now, AB || ST and EF is the transversal, so using the property, ”alternate interior angles are equal”, we get,
∠APR = ∠PRT
∠PRT = 25° .......... (1)
Similarly, CD || ST and EF is the transversal
∠QRT = ∠RQC
∠QRT = 30° .......(2)
Adding (1) and (2), we get
∠PRT + ∠QRT = 25° + 30°
x = 55°
Further,FPE is a straight line
Applying the property, angles forming a linear pair are supplementary
∠CQF + ∠CQR + ∠RQP = 180°
65° + 30° + ∠RQP = 180°
∠RQP = 180° - 95°
∠RQP = 85°
Also, applying angle sum property of the triangle
In ΔPRQ
∠RPQ + 55° + 85° = 180°°
140° + y = 180°
y = 180° - 140°
y = 40°
Thus, x = 55° and y = 40°
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
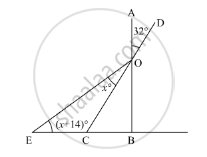
In the given figure, the value of x is ______.
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
