Advertisements
Advertisements
प्रश्न
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
उत्तर
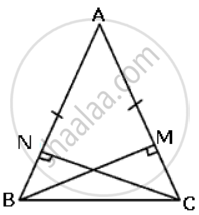
In ΔBNC and ΔCMB
∠BNC = ∠CMB = 90°
∠NBC = ∠MCB ...(AB = AC)
BC = BC
Therefore, ΔBNC ≅ ΔCMB ...(AAS criteria)
Hence, BM = CN.
APPEARS IN
संबंधित प्रश्न
If ΔPQR≅ ΔEFD, then ∠E =
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
