Advertisements
Advertisements
Question
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
Options
isosceles but not congruent
isosceles and congruent
congruent but not isosceles
neither congruent nor isosceles
Solution
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are isosceles but not congruent.
Explanation:
In triangle ABC,
AB = AC ...[Given]
∠C = ∠B ...[Angle opposite to equal sides are equal]
So, in triangle ABC is an isosceles triangle.
∠B = ∠Q ...[Given]
∠C = ∠P
∠P = ∠Q ...[Since, ∠C = ∠B]
QR = PR ...[Sides opposite to equal angles are equal]
So, in triangle PQR is also an isosceles triangle.
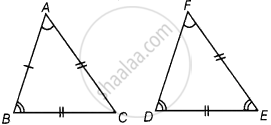
Hence, both triangle are isosceles but not congruent.
APPEARS IN
RELATED QUESTIONS
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

Show that the angles of an equilateral triangle are 60° each.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
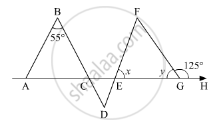
In the given figure, what is y in terms of x?

It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
Find all the angles of an equilateral triangle.
