Advertisements
Advertisements
Question
Find all the angles of an equilateral triangle.
Solution
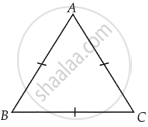
Let ABC be an equilateral triangle such that AB = BC = CA
We have, AB = AC ⇒ ∠C = ∠B ...[Angle opposite to equal sides are equal]
Let ∠C = ∠B = x° ...(i)
Now, BC = BA
⇒ ∠A = ∠C ...(ii) [Angles opposite to equal sides are equal]
From equations (i) and (ii),
∠A = ∠B = ∠C = x
Now, in ΔABC, ∠A + ∠B + ∠C = 180° ...[By angle sum property of a triangle]
⇒ x + x + x = 180°
⇒ 3x = 180°
∴ x = 60°
Hence, ∠A = ∠B = ∠C = 60°
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
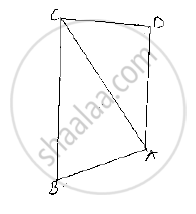
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, x + y =

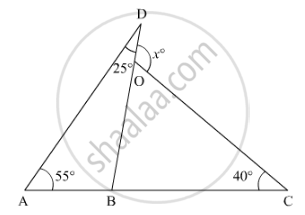
In the given figure, the value of x is ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
