Advertisements
Advertisements
Question
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Solution
Given that P is a point on the bisector of an angle ABC, and PQ|| AB.
We have to prove that ΔBPQis isosceles
Since,
BP is bisector of ∠ABC⇒∠ABP=∠PBC ............(1)
Now,
PQllAB
⇒ ∠BPQ=∠ABP ................(2)
[alternative angles]
From (1) and (2), we get
∠BPQ=∠PBC(or)∠BPQ=∠PBQ
Now,
In , ΔBPQ
∠BPQ=∠PBQ
⇒ΔBPQ is an isosceles triangle.
∴Hence proved
APPEARS IN
RELATED QUESTIONS
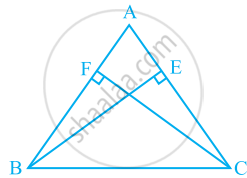
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
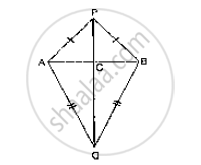
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
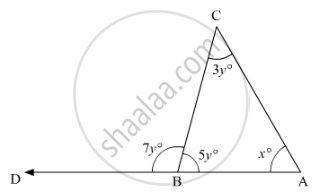
In the given figure, what is the value of x?
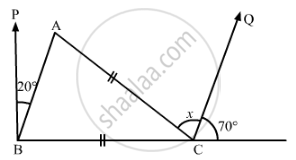
In the given figure, if BP || CQ and AC = BC, then the measure of x is
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
