Advertisements
Advertisements
प्रश्न
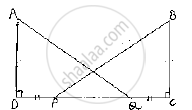
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

उत्तर
Given that, in the figure AD ⊥ CD and CB ⊥ CD and AQ = BP,DP =CQ
We have to prove that ∠DAQ=∠CBP
Given that DP= QC
Add PQ on both sides
Given that DP=QC
Add PQ on both sides
⇒ DP+PQ=PQ+QC
⇒ DQ=PC ................(1)
Now, consider triangle DAQ and CBP,
We have
∠ADQ=∠BCP=90° [given]
AQ=BP [given]
And DQ=PC [given]
So, by RHS congruence criterion, we have ΔDAQ≅ΔCBP
Now,
∠DAQ=∠CBP [ ∵Corresponding parts of congruent triangles are equal]
∴ Hence proved
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

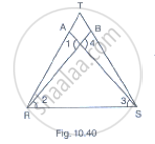
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD

