Advertisements
Advertisements
प्रश्न
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
उत्तर
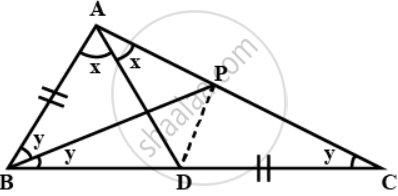
In ΔABC,
∠B = 2∠C or, ∠B = 2y, where ∠C = y.
AD is the bisector of ∠BAC.
So, let ∠BAD = ∠CAD = x.
Let BP be the bisector of ∠ABC. Join PD.
In ΔBPC, we have
∠CBP = ∠BCP = y ⇒ BP = PC
In Δ′s ABP and DCP, we have
∠ABP = ∠DCP,
∠ABP = ∠DCP = y
BP = PC ........(As proved above)
∠ADC = ∠ABD + ∠BAD
⇒ x + 2x = 2y + x
⇒ x = y
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
Find the measure of each exterior angle of an equilateral triangle.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that LN = MN.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
Write the sum of the angles of an obtuse triangle.
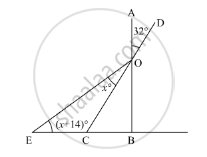
In the given figure, if AB ⊥ BC. then x =
The angles of a right angled triangle are
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
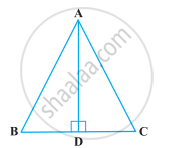
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
