Advertisements
Advertisements
प्रश्न
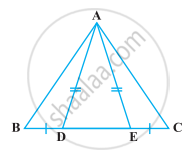
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
उत्तर

(i) ABC is an isosceles triangle in which AB = AC
∠C = ∠B ...[Angles opposite to equal sides in a triangle are equal.]
⇒ ∠OCA + ∠OCB = ∠OBA + ∠OBC
⇒ ∠OCB + ∠OCB = ∠OBC + ∠OBC
∵ OB bisects ∠B.
∴ ∠OBA = ∠OBC
And OC bisects ∠C.
∴ ∠OCA = ∠OCB
⇒ 2∠OCB = 2∠OBC
⇒ ∠OCB = ∠OBC
Now, in △OBC,
∠OCB = ∠OBC ...[Proved above]
∴ OB = OC ...[Sides opposite to equal angles]
(ii) Now, in △AOB and △AOC,
AB = AC ...[Given]
∠OBA = ∠OCA
∠B = ∠C
BO bisects ∠B and CO bisects ∠C.
∠OBA = ∠OCA
OB = OC
∴ △AOB ≌ △AOC ...[By SAS congruence rule]
⇒ ∠OAB = ∠OAC ...[Corresponding parts of congruent triangles]
So, AO bisects ∠A.
APPEARS IN
संबंधित प्रश्न
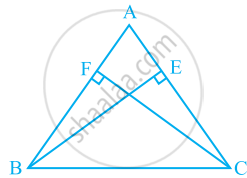
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
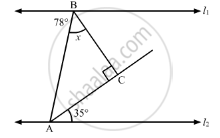
In the given figure, for which value of x is l1 || l2?
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.