Advertisements
Advertisements
प्रश्न
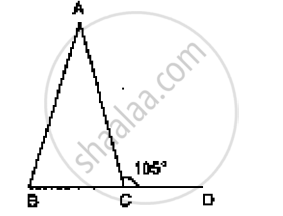
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
उत्तर

Consider the given figure
We have,
AB = AC and ∠ACD =105^@
Since,
∠BCD = 180° = Straight angle
∠BCA + ∠ACD = 180°
∠BCA +105° = 180°
∠BCA = 180° -105° ⇒ ∠BCA = 75° .......1
And also,
ΔABC is an isosceles triangle [∵AB = AC]
⇒ ∠ABC = ∠ACB
From (1), we have [Angles opposite to equal sides are equal]
∠ACB = 75° ⇒∠ABC = ∠ACB = 75°
And also,
Sum of interior angles of a triangle = 180°
⇒∠ABC = ∠BCA + ∠CAB = 180°
⇒ 75° + 75° + ÐCAB = 180°
⇒ 150° +∠BAC = 180°⇒ ∠BAC = 180° -150° = 30°
∠BAC=30°
APPEARS IN
संबंधित प्रश्न
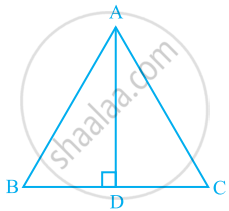
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
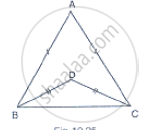
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
