Advertisements
Advertisements
प्रश्न
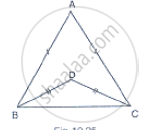
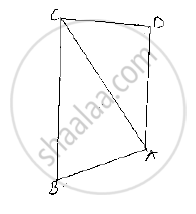
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
उत्तर
Consider the figure Given
AB = AC, DB = DC and given to find the ratio
∠ABD = ∠ACD
Now,∠ABC and ∠DBC are isosceles triangles since AB = AC and
DB = DC respectively
⇒ ∠ABC = ∠ACB and ∠DBC = ∠DCB [ ∵ angles opposite to equal sides are equal]
Now consider,
∠ABD : ∠ACD
⇒ (∠ABC - ∠DBC ) : (∠ACB - ∠DCB)
⇒ (∠ABC - ∠DBC ) : (∠ABC - ∠DBC ) [∵∠ABC - ∠ACB and ∠DBC = ∠DCB]
⇒ 1:1
∴∠ABD :∠ACD = 1:1
APPEARS IN
संबंधित प्रश्न
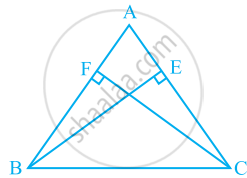
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
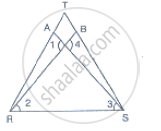
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Prove that each angle of an equilateral triangle is 60°.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
In the given figure, if AB ⊥ BC. then x =
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
