Advertisements
Advertisements
Question
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
Options
3.6 cm
4.1 cm
3.8 cm
3.4 cm
Solution
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be 3.4 cm.
Explanation:
Given, the length of two sides of a triangle are 5 cm and 1.5 cm, respectively.
Let sides AB = 5 cm and CA = 1.5 cm
We know that, a closed figure formed by three intersecting lines (or sides) is called a triangle, if difference of two sides < third side and sum of two sides > third side
∴ 5 – 1.5 < BC and 5 + 1.5 > BC
⇒ 3.5 < BC and 6.5 > BC
Here, we see that options (a), (b) and (c) satisfy the above inequality but option (d) does not satisfy the above inequality.
APPEARS IN
RELATED QUESTIONS
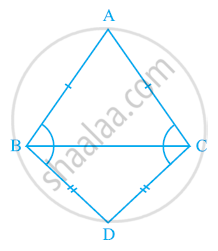
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
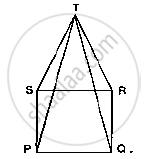
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In the given figure, x + y =

In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
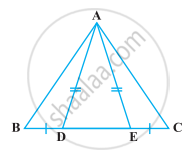
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.