Advertisements
Advertisements
प्रश्न
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
पर्याय
3.6 cm
4.1 cm
3.8 cm
3.4 cm
उत्तर
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be 3.4 cm.
Explanation:
Given, the length of two sides of a triangle are 5 cm and 1.5 cm, respectively.
Let sides AB = 5 cm and CA = 1.5 cm
We know that, a closed figure formed by three intersecting lines (or sides) is called a triangle, if difference of two sides < third side and sum of two sides > third side
∴ 5 – 1.5 < BC and 5 + 1.5 > BC
⇒ 3.5 < BC and 6.5 > BC
Here, we see that options (a), (b) and (c) satisfy the above inequality but option (d) does not satisfy the above inequality.
APPEARS IN
संबंधित प्रश्न
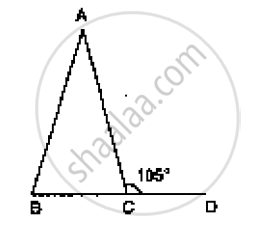
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Write the sum of the angles of an obtuse triangle.
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
Find all the angles of an equilateral triangle.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
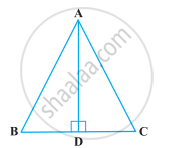
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
