Advertisements
Advertisements
Question
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
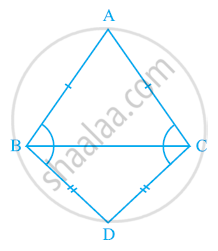
Solution
In isosceles △ABC,
AB = AC ...[ABC is an isosceles triangle]
∴ ∠ACB = ∠ABC …(i) ...[Angles opposite to equal sides of a triangle are equal]
Also, in isosceles △BCD,
BD = DC ...[BDC is an isosceles triangle]
∴ ∠BCD = ∠CBD ...(ii) ...[Angles opposite to equal sides of a triangle are equal]
On adding the corresponding sides of (i) and (ii)
∠ACB + ∠BCD = ∠ABC + ∠CBD
⇒ ∠ACD = ∠ABD or ∠ABD = ∠ACD ...(By Corresponding parts of congruent triangles)
APPEARS IN
RELATED QUESTIONS
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
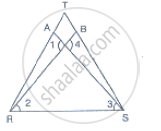
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
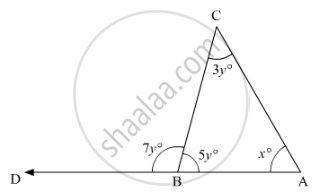
In the given figure, what is the value of x?
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
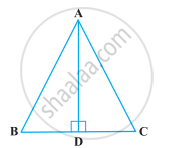
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
