Advertisements
Advertisements
Question
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Solution
ED is a straight line segment and B and C are points on it.
`⇒∠EBC = ∠BCD = straight angle = 180^@``
⇒∠EBA+∠ABC = ∠ACB +∠ACD
⇒∠EBA = ∠ACD +=ACB -∠ABC
⇒∠EBA=∠ACD [From (1) ∠ABC =∠ACD]
⇒∠ABE = ∠ACD
∴Hence proved
APPEARS IN
RELATED QUESTIONS
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
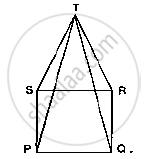
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
