Advertisements
Advertisements
प्रश्न
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Advertisements
उत्तर
In the given ΔABC,AB = ACand AB is produced to D such that BD = BC
We need to find ∠ACD : ∠ADC
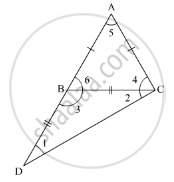
Now, using the property, “angles opposite to equal sides are equal”
As AB = AC
∠6 = ∠4 ........(1)
Similarly,
As BD = BC
∠1 = ∠2 ........(2)
Also, using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angle”
In ΔBDC
ext. ∠6 = ∠1 + ∠2
ext. ∠6 = ∠1 + ∠1 (Using 2)
ext. ∠6 = 2∠1
From (1), we get
ext. ∠4 = ∠2 .......(3)
Now, we need to find ∠ACD : ∠ADC
That is,
(∠4 + ∠2): ∠1
(2∠1 + ∠2) : ∠1 (Using 3)
(2∠1 + ∠1) : ∠1(Using 2)
3∠1 :∠1
Eliminating ∠1from both the sides, we get 3:1
Thus, the ratio of ∠ACD :∠ADC is 3 :1
APPEARS IN
संबंधित प्रश्न
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, for which value of x is l1 || l2?
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
