Advertisements
Advertisements
Question
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
Solution
Given: ABCD is a quadrilateral.
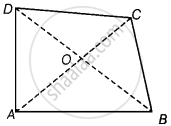
To show: AB + BC + CD + DA < 2(BD + AC)
Construction: Join diagonals AC and BD.
Proof: In ΔOAB, OA + OB > AB ...(i) [Sum of two sides of a triangle is greater than the third side]
In ΔOBC, OB + OC > BC ...(ii) [Sum of two sides of a triangle is greater than the third side]
In ΔOCD, OC + OD > CD ...(iii) [Sum of two sides of a triangle is greater than the third side]
In ΔODA, OD + OA > DA ...(iv) [Sum of two sides of a triangle is greater than the third side]
On adding equations (i), (ii), (iii) and (iv), we get
2[(OA + OB + OC + OD] > AB + BC + CD + DA
⇒ 2[(OA + OC) + (OB + OD)] > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA ...[∵ OA + OC = AC and OB + OD = BD]
⇒ AB + BC + CD + DA < 2(BD + AC)
APPEARS IN
RELATED QUESTIONS
Show that the angles of an equilateral triangle are 60° each.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Prove that each angle of an equilateral triangle is 60°.
Fill the blank in the following so that the following statement is true.
If altitudes CE and BF of a triangle ABC are equal, then AB = ....
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
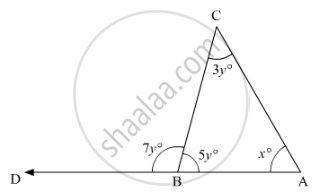
In the given figure, x + y =

In the given figure, what is the value of x?
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
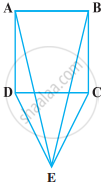
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.