Advertisements
Advertisements
Question
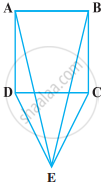
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
Advertisements
Solution
Given in figure triangle CDE is an equilateral triangle formed on a side CD of a square ABCD.
To proof that ΔADE ≅ ∆BCE
Proof: In triangle ADE and triangle BCE,
DE = CE ...[Side of an equilateral triangle]
∠ADE = ∠BCE
∠ADC = ∠BCD = 90° and ∠EDC = ∠ECD = 60°
∠ADE = 90° + 60° = 150° and ∠BCE = 90° + 60° = 150°
AD = BC ...[Sides of a square]
∆ADE ≅ ∆BCE ...[By SAS congruence rule]
APPEARS IN
RELATED QUESTIONS
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Prove that each angle of an equilateral triangle is 60°.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
Fill the blank in the following so that the following statement is true.
If altitudes CE and BF of a triangle ABC are equal, then AB = ....
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
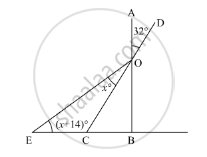
In the given figure, if AB ⊥ BC. then x =
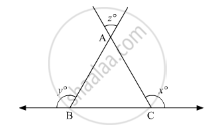
In the given figure, if BP || CQ and AC = BC, then the measure of x is
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
