Advertisements
Advertisements
Question
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
Options
4 cm
5 cm
2 cm
2.5 cm
Solution
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is 4 cm.
Explanation:
Given, ∆PQR such that ∠R = ∠P, QR = 4 cm and PR = 5 cm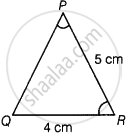
In ∆PQR, ∠R = ∠P
⇒ PQ = QR ...[Sides opposite to equal angles are equal]
⇒ PQ = 4 cm ...[∵ QR = 4 cm]
Hence, the length of PQ is 4 cm.
APPEARS IN
RELATED QUESTIONS
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
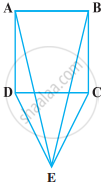
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
