Advertisements
Advertisements
Question
Prove that each angle of an equilateral triangle is 60°.
Solution
Given to prove that each angle of an equilateral triangle is 60°
Let us consider an equilateral triangle ABC
Such that AB= BC= CA
Now,
AB=BC ⇒ ∠A=∠C ................(1) [Opposite angles to equal sides are equal]
and BC = AC ⇒∠B = ∠A ……..(2)
From (1) and (2), we get
∠A = ∠B = ∠C ..............(3)
We know that
Sum of angles in a triangle =180°
⇒∠A+∠B+∠C=180°
⇒ ∠A+∠A+∠A=180°
⇒3 ∠A=180°
⇒ `∠A=(180°)/3=60°`
∴∠S=∠B=∠C=60°
Hence, each angle of an equilateral triangle is 60°.

APPEARS IN
RELATED QUESTIONS
Show that the angles of an equilateral triangle are 60° each.
Find the measure of each exterior angle of an equilateral triangle.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, if AB ⊥ BC. then x =
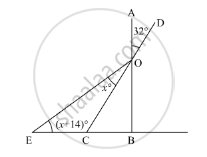
In the given figure, what is y in terms of x?

The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
