Advertisements
Advertisements
Question
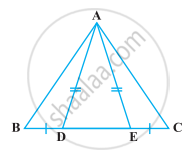
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
Solution
Given that angles A,B,C of a triangle ABC equal to each other.
We have to prove that ΔABC is equilateral We have, ∠A = ∠B =∠C
Now,
[Opposite sides to equal angles are equal]
and ∠B = ∠C ⇒ AC = AB
From the above we get
AB= BC =AC
⇒ ΔABC is equilateral

APPEARS IN
RELATED QUESTIONS
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F):
The bisectors of two equal angles of a triangle are equal
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.